多くの方にとって、「ラプラス変換」は微分方程式を解くための難解な数学ツールというイメージが強いかもしれません。
しかし、私たちのような振動試験機(加振機)を開発・製造する現場において、ラプラス変換は単なる理論ではありません。製品の「制御精度」を高め、試験の「安全性」を担保するために日常的に使用する、まさにエンジニアリングの共通言語です。
本記事では、教科書的な定義だけでなく、実際の振動制御や共振解析でどのように活用されているかという「実務の視点」を交え、Pythonによる実装方法までを解説します。
現場のエンジニアはなぜ「ラプラス変換」を使うのか?
結論から言えば、「複雑な時間変化(微分方程式)を、簡単な計算(代数方程式)に置き換えるため」です。
時間領域から周波数領域への架け橋
物理現象、特に振動や電気信号は、時間 $t$ とともに変化します。これをそのまま計算しようとすると、微分や積分が入り混じった複雑な方程式(微分方程式)を解かなければなりません。
ラプラス変換は、この時間領域の関数 $f(t)$ を、複素数領域 $s$ の関数 $F(s)$ に変換します。
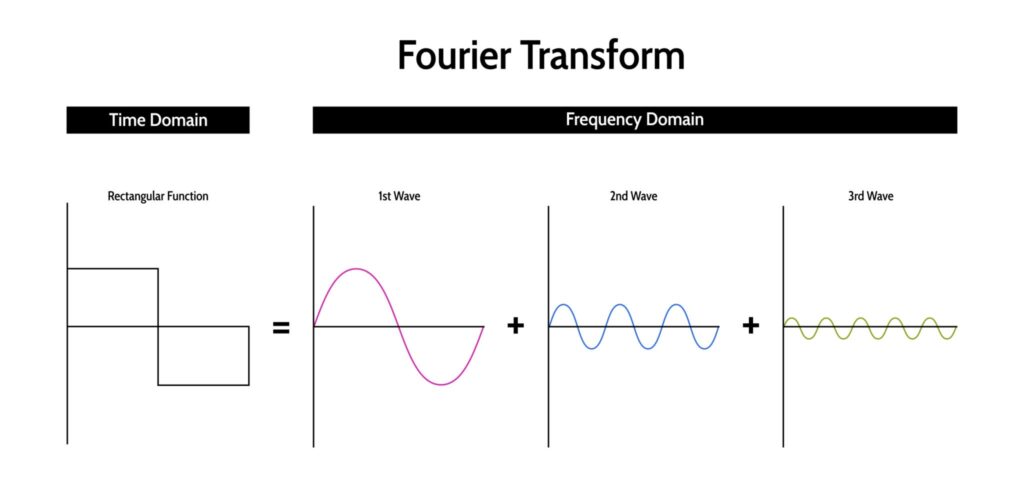
- 微分・積分の方程式 -> 掛け算・割り算の方程式
この変換により、複雑な動的システムの解析が劇的に簡略化されます 。イメージとしては、複雑な音(波形)を、音符(周波数成分)の集まりに分解して理解するプロセスに似ています 。
【実例】振動試験機開発における具体的活用
では、実際のモノづくりの現場でラプラス変換はどう役立っているのでしょうか? 当社の開発事例(振動試験機)を例に、その重要性を解説します。
1. 制御システムの「脳」を作る(PID制御)
振動試験機が、ユーザーの指定した通りの振動波形を正確に再現できるのは、高度なフィードバック制御を行っているからです。
この制御設計において、私たちはシステムの入力と出力の関係を表す「伝達関数 $G(s)$」を用います。特に、多くの制御系で採用されるPID制御の設計には、ラプラス変換の考え方が不可欠です。
- P(比例項): バネのように、現在の誤差に即座に反応する。
- I(積分項): 過去の誤差を蓄積し、定常的なズレを解消する(保持力)。
- D(微分項): 将来の変化を予測し、振動を抑えるダンパーの役割を果たす。
これらを $s$ 領域の数式(伝達関数)として記述することで、システムが暴走しないか(安定性)、狙い通りの応答速度が出るかなどをシミュレーションしているのです。
2. 「共振」による破壊を防ぐ(振動解析)
製品開発において最も警戒すべき現象の一つが「共振」です。 構造物が持つ固有の振動数と、外部からの入力周波数が一致すると、振動が増幅され、最悪の場合は破損に至ります。
私たちは、対象物を「質量 $m$、減衰 $c$、バネ定数 $k$」を持つモデル(バネ質量系)として数式化します。
$$m\ddot{x}(t) + c\dot{x}(t) + kx(t) = F(t)$$
この運動方程式をラプラス変換して解析することで、固有振動数や減衰比を正確に割り出し、共振点を回避する設計を行っています。
Python (SymPy) で解くラプラス変換の実装
現代のエンジニアは、手計算だけでなく計算ツールを活用して効率的に解析を行います。
ここでは、Pythonの数式処理ライブラリ SymPy を使って、実際にラプラス変換を行うコード例を紹介します。
減衰振動波形の変換例
減衰しながら振動する波形 $f(t) = e^{-t}\sin(2t)$ をラプラス変換してみましょう。
Python
from sympy import symbols, exp, sin, laplace_transform
# 1. 変数の定義(t: 時間, s: 複素数)
t, s = symbols('t s')
# 2. 時間関数 f(t) の定義
# e^(-t) * sin(2t) という減衰振動の式
f = exp(-t) * sin(2*t)
# 3. ラプラス変換の実行
# laplace_transform(関数, 時間変数, 変換後の変数)
F = laplace_transform(f, t, s)
# 4. 結果の表示
print(F)
# 出力結果: (2/((s + 1)**2 + 4), 0, True)
コードの解説
出力された 2/((s + 1)**2 + 4) は、数式で書くと以下のようになります。
$$F(s) = \frac{2}{(s+1)^2 + 2^2}$$
これは、減衰振動の公式通りの結果です。Pythonを使えば、このように数行のコードで複雑な関数の変換が可能となり、制御パラメータの検討や応答解析を効率化できます。
さらに詳しい「公式集」や「応用計算」を知りたい方へ
本記事では、ラプラス変換の概念と、振動試験機開発における活用事例、基本的なPython実装について解説しました。
しかし、実際の実務や研究においては、より詳細な「関数対応表」や、逆ラプラス変換を用いた「時間応答の導出」、回路網解析のための「ボード線図」の知識が必要になります。
現在、当社では社内エンジニアの研修用としても活用されている技術資料(PDF全15ページ)を、Web限定で無料公開しています。
【技術資料『ラプラス変換の基礎と応用』の収録内容】
- 【保存版】主要な関数・変換ペアの対応表(単位ステップ、指数、三角関数など)
- 微分方程式の解法ステップ(部分分数分解から逆変換まで)
- バネ質量系・RLC回路の具体的な解析手順
- ボード線図による周波数応答解析の読み方
- MATLAB / Python でのより詳細な実装コード
振動解析や制御工学に関わるエンジニア、学生の方にとって、手元に置いて辞書代わりに使える実践的な資料です。ぜひダウンロードしてご活用ください。
[ 📥 技術資料をダウンロードする(無料・PDF) ]